Binary Integer Programming: for (Armored Core) answer

When I was but a wee lad still wet behind the ears I was actually pretty good at the Armored Core games. This is a franchise of games where you build a mech, called an Armored Core (AC), out of more than 14 categories of customizable parts with dozens of parts in each category. During those days I would dream of the ultimate build – I would spend all my time trying to optimize the build to make sure it was the fastest, most durable, highest attack power, etc… Unfortunately, to optimize it manually would be practically impossible given the number of combinations of possible parts. Fast forward 20 year later I now posses the necessary skill set to do so using the help of mathematical optimization techniques and programming. I introduce…

Binary Integer Programming

Binary Integer Programming (BIP) allows to optimize for a variable (e.g. value) for a discreet set of choices (e.g. items) given a constraint (e.g. cost). For example, you are planning a vacation and have a limited budget of $1200. You want to decide whether to go on a beach trip or a mountain trip. You have two options for each type of trip: Option A and Option B. The objective is to maximize the expected enjoyment of your vacation based on the trip rating for each option, given the budget constraint. The costs and trip rating values are as follows:

Variable	Option A Cost	Option B Cost	Option A Rating	Option B Rating
Beach	$500	$600	8	9
Mountain	$700	$800	7	6

To formulate the problem as a binary integer programming problem, we need to define the objective function and the constraint.

Objective Function: Maximize 8X₁ + 9X₂ + 7Y₁ + 6Y2

Constraint: 500X₁ + 600X₂ + 700Y₁ + 800Y₂ ≤ 1200

Where we define the following binary variables as decision variables (1 if selected, 0 otherwise) for the option and destination:

• X₁: Option A for the beach trip
• X₂: Option B for the beach trip
• Y₁: Option A for the mountain trip
• Y₂: Option B for the mountain trip

Here the solution is clearly X1=1, X2=1, Y1=0, and Y2=0, which maximizes the objective function (=17) while still under budget ($1100 ≤ $1200).

BIP for Armored Core

In the following sections I define the optimization problem for Armored Core: Last Raven (AC:LR).

Binary Variables

AC:LR has 14 part categories (excluding optional part): Head, Core, Arm, Leg, Booster, FCS, Generator, Radiator, Inside, Extension, Back R, Back L, Arm R, Arm L. Each of these categories have some number of parts to choose from. A convenient choice is to represent each part category as a binary variable array, where the length of the array is the number of parts in that category. With some exception each part category can only have 1 part equipped. Given this constraint, an example of such a binary array could be X=[0 0 0 0 1] but it can not be X=[0 0 0 1 1] or any other additional 1, that is, when you sum up all the elements, it should be equal to 1. Mathematically, sum(X)<=1. For the following section lets define a symbol with a subscript that defines a binary array for a particular part category as: ℤ_part

Requisite Constraints

As mentioned, you can only have one of each body part equipped so that the sum:

Σ_partsℤ_part=1

Also an AC can only be put together given the following “physical” constraints: it can not carry more weight than the carrying capacity of the chosen legs (called “max leg weight”), it can not carry heavier weapons than the carrying capacity of the arms (called “max arm weight”), and it can not equip parts that drain more energy than the energy output of its generator. We can define the constraint problem as such:

CarryWeight ≤ MaxLegWeight⋅ℤ_leg
ArmWeight ≤ MaxArmWeight⋅ℤ_core
EnergySupply ≥ 0

where ⋅ is the dot product, ℤ_leg and ℤ_core choose the corresponding leg and core part with their max leg weight and max arm weight capacity, respectively. CarryWeight is the weight of all parts except the legs themselves. ArmWeight is determined by the weight of the arms themselves, equipped weapons on the arms, and also the extension and inside part. EnergySupply is simply the energy output value of the generator part minus the energy drain of all equipped parts.

Constraints on Metrics

An AC build will have the following metrics: Attack, Defense, Mobility, Energy Supply, Cooling, and vs ECM, which will be ranked on a letter scale (E, D, C, B, A, S) in terms of performance given its numeric value. As an important side note: when I was putting parts together by hand, no matter what I did, I could not manage to get all characteristics to be at S!

The relation between in-game parameters (e.g. solid defense and energy defense) and which metric is affected (e.g. Defense) was for the most part straightforward, however, it took extensive data collection and analysis to figure out how the numeric value of some parameters affect the ranks so I only deduced the thresholds for rank A and S. Here is the table:

Metric	Parameter	Rank A	Rank S
Attack (ATK)	TotalFirepower/10	20,000	25,000
Defense (DEF)	TotalSolidDefense + TotalEnergyDefense	3,800	4,000
Mobility (MOB)	GroundBoostSpeed	410	480
Energy Supply (ESUP)	EnergySupply + EnergyCapacity/10	9,800	10,400
Cooling (COL)	TotalCooling + TotalForcedCooling	34,000	35,000
vs ECM	TotalVSECM	820	1,000

The parameters are related to part stats in the following way:

• TotalFirepower is the sum of firepower of all equipped parts where Firepower = Attack Power × Ammo Count.
• TotalSolidDefense and TotalEnergyDefense is the sum of the solid and energy defense of all parts.
• GroundBoostSpeed depends on two parameters with a non-linear dependence on the weight of the AC: BoostPower×(106.4/4797+0.00483) if TotalWeight ≤ 4797 else BoostPower×(106.4/TotalWeight+0.00483). BoostPower is a parameter of the booster part. TotalWeight is the sum total weight of all parts.
• EnergySupply is the difference between EnergyOutput of the generator and the sum total of EnergyDrain of all equipped parts.
• EnergyCapacity depends on two parameters of the radiator: CondenserCapacity+EmergencyCapacity/3.
• TotalCooling is the radiator Cooling parameter plus the Cooling value of the AC body parts (head, core, arms, legs)
• TotalForcedCooling is the radiator ForcedCooling parameter plus the Cooling (no forced cooling parameter) value of the AC body parts (head, core, arms, legs)
• TotalVSECM is the sum total of the VS ECM value of all equipped parts (i.e. head and back radar)

First Result

Given the above we can now construct the optimization problem and solve it using the package cvxpy in Python. We need to define the constraint and the objective function to be maximized or minimized. First, we have the requisite constraints. Second, we want to ensure S rank for all metrics. Unfortunately, the hurdle is that the metric Mobility, which is determined by GroundBoostSpeed=BoostPower×(106.4/TotalWeight+0.00483), is a non-convex function due to the 0.00483 term and cvxpy can only handle convex functions. Luckily, the ratio BoostPower/TotalWeight is a quasi-convex function and can be solved using Disciplined Quasiconvex Programming using cvxpy. So the workaround is to choose the objective function to be maximized as BoostPower/TotalWeight, which if maximized would also maximize GroundBoostSpeed and hopefully reach the value above which we get S rank for mobility (since we can’t enforce the constraint). Running my Python code (available on GitHub) the script took about 30 seconds and produced the following build:

Category	Part
Head	H10-CICADA2
Core	CR-C83UA
Arm	YA10-LORIS
Leg	LH05-COUGAR
Booster	CR-B83TP
FCS	CR-F75D
Generator	KUJAKU
Radiator	CR-R92
Inside	CR-I86FMM
Extension	IWATO
Back R	WB03R-SIREN
Back L	CR-WB72RO2
Arm R	WR04M-PIXIE2
Arm L	CR-WH01HP

The calculated metrics are:

Metric	Value (Rank)
ATK	25068 (S)
DEF	4004 (S)
MOB	396.7 (<A)
EN SUP	10613 (S)
COOLING	35001.7 (S)
VS ECM	1008 (S)

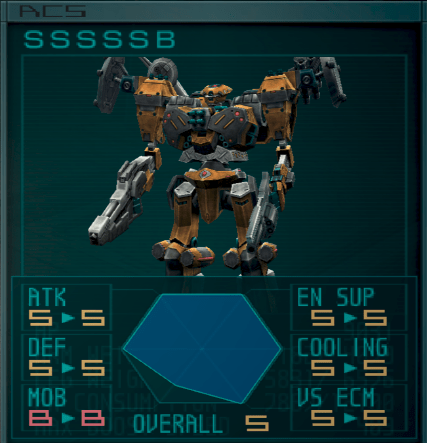
This build is not too bad, despite B rank mobility it is actually quite mobile. The biggest contributors to ATK is the rockets and floating mines – both of which are really hard to actually hit anything with.

Tuning

It is nice to see all these Ss but unfortunately we couldn’t get MOB to reach S rank. Fortunately, AC:LR has the tuning function, which allows one to optimize the equipped parts by modifying its properties slightly, such as decreasing its weight or increasing its defense stat. The limitation is that there are only 10 units of tuning per part that can be applied so it has to be redistributed among the different tuning categories strategically.

Again, using extensive data collection I figured out some relationships between the degree of tuning, an integer value between 0 and 10, and the effect it has on the stat:

Weight Tuning

I noticed there is a linear relationship (with a constant) between the initial weight of the part and the tuned weight at a given tuning value:

where and is the untuned and tuned weight of the part, respectively. and is the slope and constant in the linear relationship that depends on the variable, , which is the degree of tuning, as shown in the following graphs:

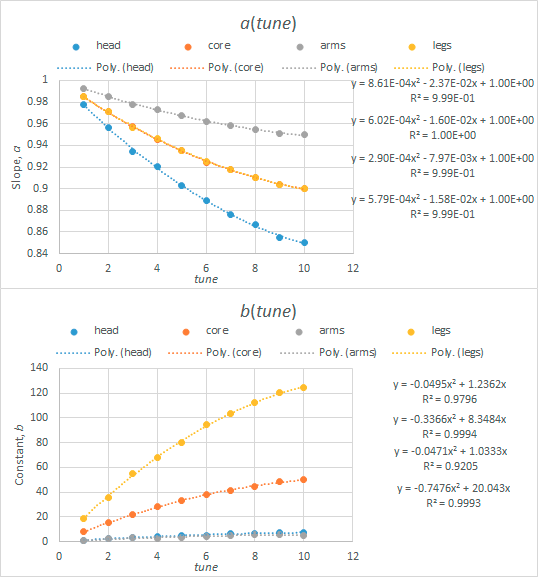
The curve fits aren’t perfect but the maximum error is about one unit for the tuned parameter. We notice that the relation between tuned and tuned value is non-linear with respect to the tune value. How this is accounted for in the convex optimization will be addressed in the appendix.

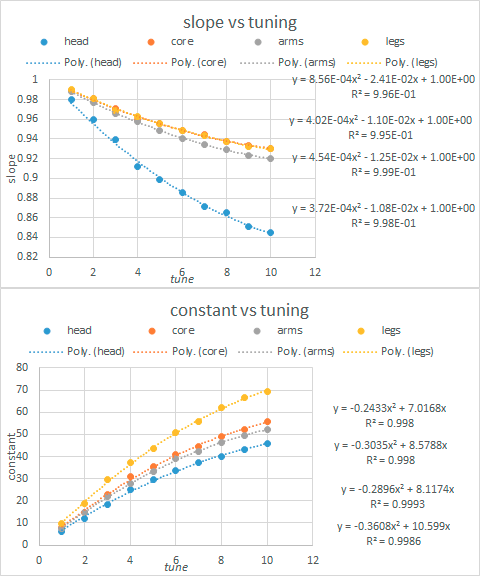
Maximum Leg Weight

All tuned parameters have the same slope vs tune and constant vs tune functional relation as with weight. The slope and constant are as shown:

Solid Defense

Results as follows:

Energy Defense

Results as follows:

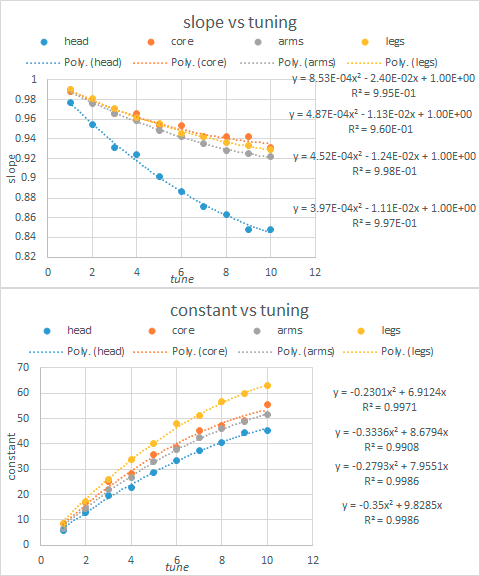
This was the last parameter I determined as this whole process was too time intensive. However, just the weight and defense parameters will turn out to be sufficient!

S-rank Result

After incorporating tuning into the optimization process (see appendix for non-trivial details) I managed to produce the following AC:

Category	Part
Head	CR-H05XS-EYE3
Core	CR-C83UA
Arm	YA10-LORIS
Leg	LN04-WALRUS2
Booster	unequipped
FCS	CR-F75D
Generator	KUJAKU
Radiator	CR-R92
Inside	CR-I86FMM
Extension	IWATO
Back R	CR-WB69RO
Back L	WB10R-SIREN2
Arm R	WR07M-PIXIE3
Arm L	YWH14PU-ROC4

Metric	Value (Rank)
ATK	25060.8 (S)
DEF	4000.4 (S)
MOB	478.5 (A)
EN SUP	10824 (S)
COOLING	35313.3 (S)
VS ECM	1016 (S)

Again I could not get S rank on MOB… However, in-game I could still tune the generator and radiator weight and I managed to get the following:

S-rank-on-all-metrics! With weight sufficiently reduced the max boost speed (ground boost speed) increased to 498 – enough to S rank. Hilariously enough, despite the metrics, this build is quite bad and can’t boost in the air for long without overheating. In some sense, this was an exercise in proving that these metrics don’t translate to actual battle performance!

Appendix

Convex Optimization with Part Tuning

Including tuning in the optimization was not straightforward at all. As shown previously, the relation between tuned parameter and the degree of tuning is non-linear (thus non-convex) due to the quadratic dependence. Convex optimization can NOT solve this situation so I had to find a way to linearize the problem.

The solution was to consider a tuned part to be the same as a unique part in of itself. Since the tune parameter takes a discreet value between 0 and 10 it is like saying we have 11 unique parts – each with its tune adjusted values. For example, the weight value of a head part:

tune	0	1	2	3	4	5	6	7	8	9	10
weight	514	504	494	484	477	469	462	457	452	447	444

Since there is initial weight dependence on the final tuned value, this array has to be generated for each head part. There are 28 head parts to choose from, with the tuning, this will make it 28×11=308 “tuned” head parts to choose from. This combination is best represented as a two-dimensional matrix:

199	241	222	143	230	293	189	228	387	141	362	199	330	315	184	202	260	343	262	514	197	228	179	241	101	468	435	145
196	237	218	141	226	287	186	224	379	139	355	196	324	309	181	199	255	336	257	503	194	224	176	237	100	458	426	143
193	233	215	139	222	282	183	220	372	137	348	193	318	303	178	195	251	330	253	494	191	220	173	233	99	450	418	141
190	229	211	137	219	278	180	217	366	135	342	190	312	298	176	192	247	325	249	485	188	217	171	229	98	442	411	139
187	226	208	136	216	273	178	214	360	134	337	187	307	294	173	190	243	319	245	477	185	214	169	226	97	434	404	137
185	223	205	134	213	270	176	211	354	132	332	185	303	289	171	187	240	315	242	469	183	211	167	223	96	428	398	136
183	220	203	133	210	266	174	208	350	131	327	183	299	286	169	185	237	310	238	462	181	208	165	220	95	422	392	135
181	217	201	132	208	263	172	206	345	130	323	181	295	282	167	183	234	307	236	457	179	206	163	217	95	416	387	133
179	215	199	130	206	260	170	204	342	129	320	179	292	279	166	182	232	304	233	452	177	204	162	215	94	412	383	132
178	214	197	130	204	258	169	202	339	128	317	178	290	277	165	180	230	301	232	447	176	202	160	214	94	408	380	131
176	212	196	129	203	256	168	201	336	127	315	176	288	275	164	179	228	299	230	444	175	201	159	212	93	405	377	131

Lets represent the above matrix as where and are the row and column indices starting from 0. So in the above matrix.

Note that the above procedure has to be done for each category of tuned parameter, i.e. the energy defense, shell defense, etc… So we would have where and where , which would correspond to the solid and energy defense tuning, respectively.

Since now we are working with matrices we can not use our binary arrays for part selection. We have to create a binary matrix , where selects the part (head, core…), selects the category to tune (weight, shell defense,…), and selects the tune value (0, 1, …). So for head part with the three tuning categories we will have , , and . For example, if we choose the 2nd head part with a tune of 2, , it will look like this:

0	0	0	…	0
0	0	0	…	0
0	1	0	…	0
…	…	…	…	0
0	0	0	0	0

With the addition of all these new variables that are used in the optimization we have to properly define the constraints. As shown in the above example, there can only be one non-zero element (and it must be =1).

The total tune across tune categories for a part must be no larger than 10.

Lastly, the choice of part for each tune category must be the same (e.g. we can not have two different head parts equipped simultaneously). The best way to enforce this constraint is to keep the old binary array and let our binary matrices for each category equal it by summing across the rows:

Using the Python Script

To generate your own optimized build get the Python script from my GitHub. You will need to install the numpy, pandas, and cvxpy (version 1.3.1 or greater) packages. Lastly, you will need to get the data from the Google Sheet file “Armored Core: Last Raven (PS2+PSP) – Parts Reference Sheet by iWantYourSmiles/FenLupis” and export the sheets as .tsv files into the parent directory of this script. The files to load are:

• ACLR_Head.tsv
• ACLR_Core.tsv
• ACLR_Arm.tsv
• ACLR_Leg.tsv
• ACLR_Booster.tsv
• ACLR_Generator.tsv
• ACLR_Radiator.tsv
• ACLR_FCS.tsv
• ACLR_Weapon.tsv
• ACLR_Back.tsv
• ACLR_Extension.tsv
• ACLR_Inside.tsv

At the top of the script we have some options selected by 1 or 0 for not selected:

The script lets you choose the SCIP solver, which seems generally faster than the default but it needs to be installed. The script can exclude parts from AC:Last Raven if considering only AC:Ninebreaker. The “OP” variables enable/disable optional parts.

The objective function is controlled by (un)commenting some lines of code (only 1 can be uncommented!):

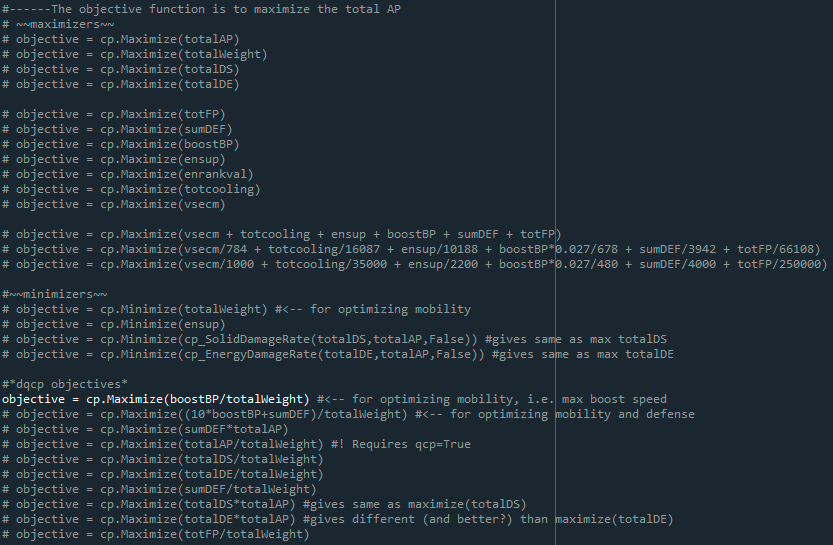
The variable names and functions are somewhat self-explanatory – cp.Maximize(totalAP) will maximize the total AP of the AC. More complicated objective functions are shown under the *dqcp objectives* where it is optimizing a ratio or a multiplication of two convex function. This produces a quasi-convex objective function, which Disciplined Quasiconvex Programming can solve.

Special constraints for ensuring a specific rank of a metric is also done by (un)commenting some lines of code:

In the above image the constraints for all metrics is S rank.

P.S.

At the onset this “fun idea” seemed very straightforward and thought it would be done fairly quickly. However, there was a lot of work to determine the functional relations due to tuning and even the metrics took some work to determine. Initially I hoped to implement everything, such as tuning of other parameters and for other parts too, but I had achieved the all-S-rank AC with what I had. So I felt I had achieved my childhood dream and I am satisfied with the work done.

As for future prospects, it may be that the all-S-rank AC I found is not the only configuration. Incorporating tuning for other parts might possibly find another configuration. Also, to make a more practical AC it might be useful to “ban” some parts from the optimization process (e.g. rockets, floating mines).

Acknowledgements

• The stats/parameters for the AC parts (and O04-GOLGI numeric effect) were taken from the Google Sheet file “Armored Core: Last Raven (PS2+PSP) – Parts Reference Sheet by iWantYourSmiles/FenLupis“
• Found the equation for the parameter GroundBoostSpeed in the page source of The Raven Republic AC:LR builder
• The numeric effect for MARISHI optional part was taken from the Japanese Armored Core wiki – ARMORED CORE @ ウィキ
• FromSoftware for making the awesome Armored Core games